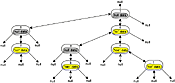
Figure 1. An English dictionary built on a ternary search tree TST structure
From an external perspective, the TST behaves like a HashMap or a HashTable. That is, objects stored in the tree are indexed using string keys. Internally, the TST stores each key character in a separate node.
Figure 2. A ternary search tree Click on thumbnail to view full-size image. (19 KB) Figure 2 illustrates two types of objects: objects that represent tree nodes (no color) and value objects (yellow or gray) encapsulated by the nodes. Arrows represent references — if a bidirectional arrow connects nodes “s” and “o,” then “s” has a reference to “o,” and “o” has a reference to “s.” Each TST node encapsulates one character from a key (its splitchar), one value object, a reference to its parent node, and a reference to each of three child nodes — lo kid, equal kid, and hi kid. A lo kid is below and to the left of its parent, an equal kid is directly below its parent, and a hi kid is below and to the right of its parent. The highest node in the tree is the root node; its parent is null.
The TST in Figure 2 stores five key-value pairs. The keys are so, tab, to, too, and tot. The string too, for example, points to an instance of an object labeled too data in the diagram.
TST algorithms
Let’s turn to the manipulation of data stored in the TST. You need a means for using a string key to retrieve data from the tree, using a string key to insert data into the tree, retrieving any data whose key matches a given prefix, and for retrieving any data whose key closely matches a given string.
The following algorithm retrieves the object indexed by a string key.
Object get(String key) {
TSTNode currentNode = rootNode;
int charIndex = 0;
while(true) {
if(currentNode == null) return null;
if (key.charAt(charIndex) == currentNode.splitchar) {
charIndex++;
if(charIndex == key.length()) return currentNode.data;
currentNode = currentNode.relatives[TSTNode.EQKID];
} else if(key.charAt(charIndex) < currentNode.splitchar) {
currentNode = currentNode.relatives[TSTNode.LOKID];
} else {
currentNode = currentNode.relatives[TSTNode.HIKID];
}
}
}
Within a given iteration, this algorithm focuses on a certain node within the tree — the currentNode — and on a certain character within the key — though not explicitly named above, let’s call it currentChar.
If currentChar comes before the currentNode‘s splitchar in the alphabet, the algorithm shifts its focus to the currentNode‘s lo kid, does not change the value of currentChar, and repeats the process. If currentChar comes after the currentNode‘s splitchar, the algorithm shifts to the currentNode‘s hi kid, does not change currentChar‘s value, and repeats the process. If currentChar is equal to the currentNode‘s splitchar, the algorithm shifts to the currentNode‘s equal kid, sets the value of currentChar to the next char in the key, and repeats the process. When the currentChar‘s value changes, the algorithm checks to see if the end of the key has been reached; if it has, it returns the data object — the value — stored in the currentNode.
Refer back to Figure 2 as I walk you through the process of retrieving the data indexed by tab. First, set currentChar to the first letter in the key — tab — and set currentNode to the root node — the “t” node, or highest node in Figure 2. Compare currentChar with the rootNode‘s splitchar; since both are equal to “t,” shift to the “o” node and set currentChar to the next character in tab. Since “a” comes before “o” in the alphabet, move to the lo kid — the “a” node.
Since both currentChar and splitchar are now “a,” move to the equal kid — the “b” node — and set currentChar to the next character in tab. Now, both currentChar and splitchar equal “b.” You’ve reached the end of the key, so the data object stored in the “b” node is the data you’re after.
Consider the problem of storing the key-value pair: tab, myObject. To store the pair, you can use the same algorithm with one slight modification — once it finds the tab node, instead of returning the data object, the algorithm stores myObject in the node (overwriting any data already stored in that node).
Suppose you wish to store a key-value pair and the tree lacks some or all of the nodes required to represent the key. Again, you use nearly the same algorithm. Upon entering a new iteration of the while loop, if the currentNode is null, simply create the missing node and add it to the tree. The new node’s position should be the position in which you expected to find it.
Say you wish to store tub, myObject in Figure 2’s tree. Set currentChar to the key’s (tub) first character, and set currentNode to the root node. Compare currentChar to the currentNode‘s splitchar; since both equal “t,” set currentChar to the next character in tub and set currentNode to the equal kid — the “o” node. Compare currentChar to “o.” Since “u” comes after “o” in the alphabet, set currentNode to the hi kid, leaving currentChar unchanged. Since currentNode is null, create a new node, setting its splitchar to currentChar, “u.” The new node will become the “o” node’s hi kid. Now compare currentChar to the currentNode‘s splitchar; since both equal “u,” set currentChar to the next character in the key and currentNode to the equal kid. Because currentNode is null, create a new node, setting its splitchar to currentChar, or “b.” The new node will become the “u” node’s equal kid. Compare currentChar to the currentNode‘s splitchar; both are equal to “b.” You’ve reached the end of the key, so store myObject in currentNode — the “b” node. Figure 3 depicts the new tree structure.
Figure 3. Figure 2’s TST after adding tub key. Click on thumb- nail to view full size image. (23 KB) The example described above highlights an important characteristic of the TST data structure: Though tub has three characters, adding its key resulted in the addition of only two new tree nodes. That results because the TST reuses the “t” node (root node in Figure 2) in the representation of the new key, tub. Similarly, if you add a new key tool, only one more node (splitchar equal to 'l') would be required. Because the TST reuses nodes and because it creates nodes only when needed to represent new keys, the TST occupies little memory relative to many other data structures.
You’ve examined the basic storage and retrieval of data. Now explore how to find data having keys that only partially match a target string.
To find all nodes whose keys have a given prefix, simply find the node indexed by that prefix. Regard that node’s equal child as a subtree’s root node. Every node in the subtree represents a key that begins with the prefix. Since the tree (or subtree) structure maintains the alphabetical order of its keys, a recursive algorithm that retrieves a list of tree data will order the list according to the keys’ alphabetical order.
What does it mean to find all nodes whose keys nearly match a target string? In this case, keys can differ from a target string by a specified number of characters. For example, impliment differs from implement by one character. An algorithm that implements that functionality can form the basis for dictionary spell-checking. The recursive algorithm below finds all keys differing from the target key by “d” characters:
matchAlmost(String key, int i, TSTNode currentNode, int d) {
if((currentNode == null) || (d < 0) || (i == key.length())) return;
// low branch
if(key.charAt(i) < currentNode.splitchar) matchAlmost(key, i, currentNode.relatives[TSTNode.LOKID], d);
//equal branch
int nextD = (key.charAt(i) == currentNode.splitchar) ? d : d - 1;
if((key.length() == i + 1) && (nextD == 0) && (currentNode.data != null)) {
// add the key of the current node to the list of nearly matching keys
}
matchAlmost(key, i + 1, currentNode.relatives[TSTNode.EQKID], nextD);
// hi branch
if(key.charAt(i) > currentNode.splitchar) matchAlmost(key, i, currentNode.relatives[TSTNode.HIKID], d)
}
The algorithm above resembles the algorithm for finding matching keys, except that it regards a key character (currentChar) as matching a currentNode‘s splitchar when the characters actually match or when the current number of mismatching characters has not exceeded the desired number. Unlike the algorithm used in the get method, the algorithm above is recursive and can return multiple values.
Flexible arrays
You may use a TST as an array of type Object. Simply convert the array index to a string and regard it as a TST key. For example, to store myObject into slot int i = 79, call myTST.put(String.valueOf(i), myObject);. You can easily wrap a TST in a class that automatically performs the int-to-string conversion. It isn’t necessary to declare the capacity of such an array in advance — that is, when the array instantiates.
You can use an arbitrary separator (say, 'u0800') to separate indices of multidimensional arrays. For example, to add another index int j = 7 to the prior example, call myTST.put(String.valueOf(i) + 'u0800' + String.valueOf(j), myOtherObject). Just as it isn’t necessary to declare the capacity of such an array in advance, it isn’t necessary to declare its dimensions in advance either. In fact, a one-dimensional array can occupy the same TST as other multidimensional arrays. In that case, an array’s data with a specific dimension will not overwrite those arrays having other dimensions.
A TST database
Let’s use a TST to build the following database:
A simple database
Employee ID
Employee eye color
Employee hair color
33
Blue
Blue
37
Brown
Brown
Use special marker characters (e.g., 'u0800', 'u0801', and so on) for a TST node’s splitchar to identify database columns. Figure 4 depicts a database with three columns and two entries. The columns are employee ID ('u0800'), employee eye color (u0801), and employee hair color ('u0802').
Figure 4. A TST database Click on thumbnail to view full-size image. (25 KB) The column identified by the splitchar 'u0800' contains an integer ID that is unique for each employee, like a social security number. Such values are known as primary keys. The ID entry for person number 33 is added to the database with the statement myTST.put(String.valueOf(33) + 'u0800', emp33DBEntry), where emp33DBEntry is an instance of a DatabaseEntry class (described below). Placing the marker characters at the end of the keys, rather than at the beginning, allows columns and entries to share TST nodes, thus reducing the memory occupied by the database.
As depicted in Figure 4, an instance of the DatabaseEntry class will be stored in one employee ID node, a 'u0800' node. The same DatabaseEntry instance will also be stored in two linked lists. One of these lists will reside in an eye color node — a 'u0801' node — and the other in a hair color node — a 'u0802' node. The database entry object has a handle to the TST node that terminates its primary key column entry, the 'u0800' node. It also has a handle that points to the LinkedList node storing its eye color entry and another handle that points to the LinkedList node storing its hair color entry. Each of these LinkedList nodes has static handles to the TST nodes that encapsulate the LinkedLists. That allows you to decipher the column value by walking the tree backwards until you reach the root node.
To retrieve the hair color of employee 37, obtain the database entry object indexed by the string "37" + 'u0800'. From this database entry object, obtain the hair color LinkedList node; from this node, obtain the encapsulating TSTNode, 'u0802'. From 'u0802', walk backwards up the tree, reconstructing the hair color value as you go.
Suppose you want to set employee 33’s eye color to blue. Before storing a value in a nonprimary key column, you must verify that the value does not already exist. First, retrieve employee 33’s DatabaseEntry object: emp33DBEntry = myTST.get(String.valueOf(33) + 'u0800'). This object encapsulates a handle to a LinkedList node for the eye-color entry, and you can easily delete the node. Now call myTST.put(String.valueOf("blue") + 'u0801', emp33DBEntry). Don’t forget to reset the eye-color handle that lives in emp33DBEntry so that it points to the new LinkedList node.
To attain the employee ID for every employee having blond hair and blue eyes, retrieve the linked list indexed by the string "blond" + 'u0802' and the linked list indexed by the string "blue" + 'u0801'. Check the length of these lists and discard the longer one. Suppose the blond hair list is the shorter list. Obtain the TST node indexed by the string "blue" + 'u0801', the “blue-eye” node. Now for each entry in the blond hair list, retrieve the DatabaseEntry object and check to see if its eye-color handle references a LinkedList node that lives in the blue-eye node. If its eye-color handle does indeed reference the blue-eye node, then add the DatabaseEntry object’s employee ID to the result list, otherwise move on to the next node.
Using the same list of words I used to build the dictionary applet, I built a database similar to the one described above. Like the dictionary applet, this database featured about 48,000 entries. The word list served as the set of primary keys that uniquely identify employees. As each database entry was created, I used Java’s random number generator — Math.random() — to choose one of three values for eye color and one of three values for hair color. This algorithm produces about 16,000 (48,000/3) people having each eye color and about 16,000 people having each hair color. About 5,333 (48,000/(3*3)) people will have a given combination of hair color and eye color. Running on my 600MHz laptop, the algorithms described above take about 100 milliseconds to return a list of roughly 5,333 people having a certain hair and eye color.
While Figure 4’s database has only a single table, it isn’t difficult to devise a TST database structure that supports multiple tables.
Conclusion
The ternary search tree (TST) behaves like a HashTable, in that it uses a key to quickly locate, store, and retrieve data. TST keys are stored (and thus retrieved) in sorted order. A HashTable can use any Object as a key, as long as the object implements a hash function. In contrast, a TST must use a string key. A TST is superior to a HashTable in its ability to find data having keys that partially match a target string. Furthermore, a TST allocates no memory for data that has yet to be placed in the tree and reuses nodes (memory) that multiple data values have in common, thus reducing memory requirements for large data amounts. The flexible way in which the TST searches for and accesses data provides numerous opportunities for creative programming.